Proporcional, Integral Derivativo
El lazo PID, Proporcional Integral y Derivativo, es un algoritmo usado para controlar sistemas con una entrada y una salida analógicas. Se ha convertido en el algoritmo más popular para este fin. Muchos controladores ya lo incluyen como una instrucción de su conjunto de instrucciones.
En un lazo PID están involucrados algunas variables tales como:
- La variable de proceso (vp) o variable que se quiere controlar
- La referencia o consigna (r), es el valor que se desea que tenga la variable de proceso
- La variable de control (vc), es la señal que ordena al actuador modificar el estado de la variable de proceso.
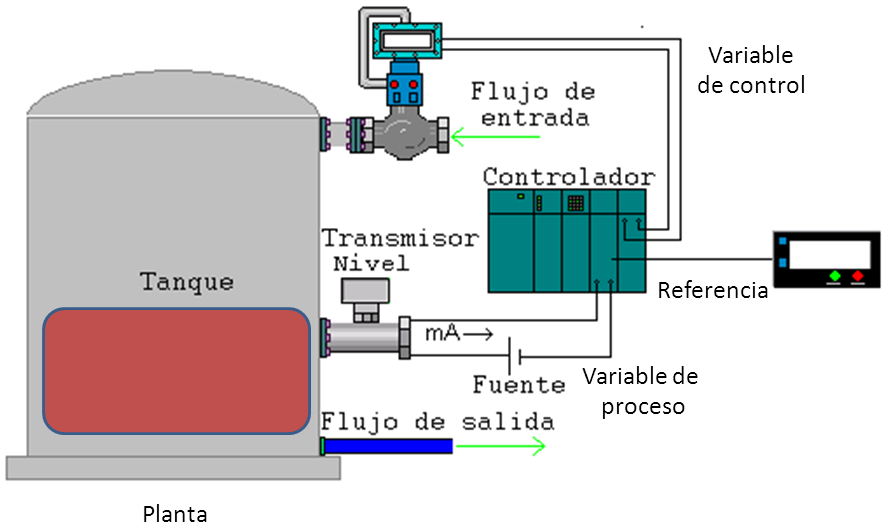
En la figura 1, se muestra un ejemplo del control de nivel de un tanque. En el ejemplo se puede apreciar: un transmisor de nivel, cuya salida es la variable de proceso; un panel de operación por medio del cual el operador configura el valor de la referencia; un controlador en el cual se ejecuta el algoritmo PID y una válvula proporcional que modifica el flujo de entrada del tanque haciendo que el valor del nivel sea mayor o menor. En este ejemplo, si el nivel está por debajo del valor de referencia, el algoritmo PID incrementa la variable de control para abrir la válvula en incrementar el flujo de entrada, lo que hace que el nivel se incremente.
Figura 1. Control de nivel del tanque
Error del sistema
Internamente el controlador calcula la señal error (e) como la diferencia entre el valor de referencia y la variable de proceso (e = r-vp). La señal error es la entrada al algoritmo PID, el cual el cual se resume a resolver la ecuación:
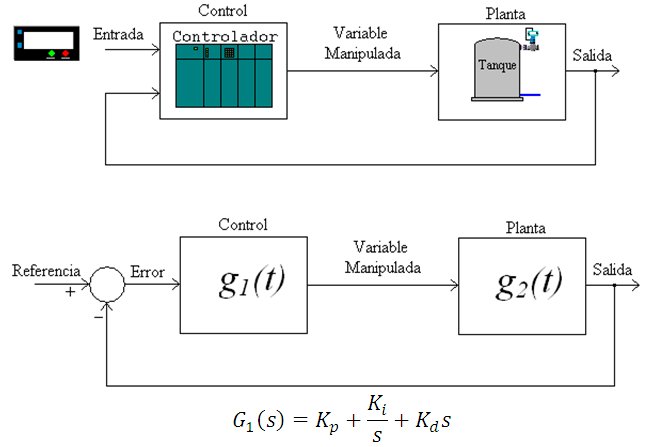
Explicar cómo funciona el algoritmo implica profundizar en la teoría de control. En la figura 2 se muestra el sistema, en él se aprecian los bloques de control y la planta. La función de transferencia g1(t) es el algoritmo PID y la función de transferencia g2(t) es la resultante de las dinámicas del tanque y la válvula de control.
Figura 2. Diagrama de bloques
Algunas variantes en la ecuación PID
Modos de acción
La ecuación PID puede tener algunas variantes. En el ejemplo del tanque, si se cambia de lugar la válvula y se coloca en la salida del tanque en lugar de en la entrada de tanque, la válvula controlaría ahora el flujo de salida. Si la variable de proceso, el nivel para el ejemplo, es menor que el valor de referencia, ahora se necesita cerrar la válvula para que el nivel incremente su valor. Este caso es conocido como modo de acción directo y el error se calcula ahora como e = vp-r, a diferencia del modo anterior el cual es llamado modo de acción inverso.
Ganancias dependientes
Si en la ecuación de PID se saca como factor común la constante proporcional, la ecuación se ve como sigue:
Donde Ti es llamado tiempo integral y Td es llamada tiempo derivativo. En esta ecuación las tres ganancias, proporcional, integral y derivativo, dependen de Kp. A esta forma de la ecuación se le denomina ecuación de variables dependiente, a diferencia de la ecuación anterior que es conocida como ecuación de variables independientes.
Bias y la derivada de la variable de proceso
En ocasiones se puede requerir que desplazar el valor de la variable de control. Esto se hace sumando un valor al cual se le denomina bias. Si el valor de la referencia es constante, entonces la derivada del error es igual a la derivada de la variable de proceso, así que la ecuación PID también puede verse de la siguiente manera.
Sintonizar un lazo PID
La finalidad del lazo es hacer que el valor de la variable de proceso sea igual al valor de referencia. El algoritmo funciona adecuadamente cuando tiene el valor correcto de las ganancias proporcional, integral y derivativa. Esto es lo que se conoce como sintonizar el lazo.
En todo proceso de sintonizar se cambia los valores de las constantes, se varía el valor de referencia y se mide la respuesta. Es un proceso que puede ser iterativo, dependiendo de las herramientas con que se cuenten y la información que se tenga del proceso.
Hay varias forma de sintonizar un lazo. Existen software diseñados para esto, los cuales estiman las dinámicas del proceso por la respuesta obtenida ante la variación de la referencia. Otros métodos están basados en la teoría de control, como por ejemplo el de Zieglers y Nichols. Estos métodos son una buena alternativa pero, en ocasiones requieren llevar al proceso a condiciones que en la práctica no son posibles, como hacer que el sistema se haga oscilatorio. También es posible que se requiera tener información de las contantes de tiempo de la planta. En algunos casos se requiere alguna inversión en dinero adicional, como en el caso del software, que necesita ser comprado. A mi entender el mejor de los casos es cuando el fabricante de las planta te suministra el valor de las constantes que debes colocar en el algoritmo, lamentablemente, esto casi nunca ocurre.
En conclusión, la mayoría de las veces en la que tenemos que sintonizar un lazo PID, debemos hacerlo de forma manual, o al menos en mi experiencia. Vamos a mostrar como sintonizar un lazo de forma manual. Primero mostraremos algunas características importantes en una gráfica de respuesta de un lazo PID.
Característica de las respuesta a un Lazo PID
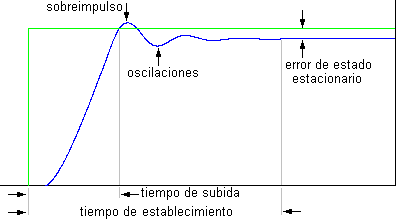
La figura 3 muestra una gráfica con la repuesta típica de la variable de proceso en una lazo PID. En la figura se puede apreciar algunas características como lo son: el sobre impulso, oscilaciones, el error en estado estacionario, y los tiempos de subida y establecimiento. El sobre impulso y las oscilaciones son síntomas de la estabilidad del sistema. El tiempo de subida y establecimiento nos indican la velocidad de respuesta, en un sistema ideal se necesita que sea estable, rápido y con cero error.
Figura 3. Respuesta del lazo PID.
Sintonizar manualmente un lazo PID
A continuación se describe el procedimiento para sintonizar el lazo PID:
- Se colocan todas las constantes a cero.
- Se incrementa la constante proporcional hasta que obtener una respuesta lo más parecido a la respuesta deseada. En este punto es posible que aparezca sobre impulso u oscilaciones,. Probablemente el error en estado estacionario sea diferente de cero.
- Para corregir el error en estado estacionario se debe ajustar la constante integral. Es posible que aumenten el sobre impulso y las oscilaciones.
- Para reducir el sobre impulso y las oscilaciones se ajusta la constante derivativa.
El siguiente video muestra un ejemplo de cómo sintonizar el lazo PID del ejemplo del tanque.
I truly appreciate this post. I抳e been looking everywhere for this! Thank goodness I found it on Bing. You have made my day! Thx again
I’m curious to find out what blog platform you happen to be using?I’m having some small security issues with my latest blog and I’d like to find something more safe.Do you have any recommendations?
cloriquine idrossiclorochina chloroquine tab
apartments in elkhorn ne northstar apartments how to soundproof an apartment
rybelsus pill – vardenafil price periactin uk
Appreciate you sharing, great blog article.Thanks Again. Really Great.
Really informative post.Really thank you! Keep writing.
meds from india: online medications from india usa pharmacy india
Great post.Really thank you! Much obliged.
It’s enormous that you are getting ideas from this article as well as from our discussion made at this place.
augmentin ca – cymbalta 40mg for sale order cymbalta pills
At this time I am ready to do my breakfast, later than havingmy breakfast coming again to read further news.
What¦s Taking place i am new to this, I stumbled upon this I’ve found It positively helpful and it has aided me out loads. I hope to contribute & help other users like its helped me. Good job.
Im obliged for the post.Really thank you! Keep writing.
I appreciate, result in I found exactly what I was looking for. You’ve ended my four day lengthy hunt! God Bless you man. Have a great day. Bye
There is visibly a lot to realize about this. I assume you made various nice points in features also.
Hmm is anyone else encountering problems with the pictures on this blog loading? I’m trying to find out if its a problem on my end or if it’s the blog. Any responses would be greatly appreciated.
order acticlate generic – buy albuterol generic glucotrol 10mg cost
I really like what you guys are up too. This sort of clever work and reporting!Keep up the excellent works guys I’ve included you guysto our blogroll.
Excellent goods from you, man. I have understand your stuff previous to and you are just extremely great. I actually like what you have acquired here, certainly like what you’re saying and the way in which you say it. You make it enjoyable and you still take care of to keep it wise. I can’t wait to read much more from you. This is actually a wonderful website.
I am curious to find out what blog system you have been utilizing? I’m experiencing some small security problems with my latest blog and I would like to find something more secure. Do you have any recommendations?
couches for small apartments rentberry scam ico 30m$ raised the edge apartments
I love your blog.. very nice colors & theme. Did you design this website yourself or did you hire someone to do it for you? Plz answer back as I’m looking to create my own blog and would like to find out where u got this from. appreciate it
You are a very clever individual!
Good day! This is my first comment here so I just wanted to give a quick shout out and tell you I really enjoy reading through your posts. Can you recommend any other blogs/websites/forums that deal with the same topics? Thank you so much!
I like the valuable information you provide in your articles. I’ll bookmark your blog and check again here regularly. I’m quite certain I’ll learn a lot of new stuff right here! Best of luck for the next!
Do you mind if I quote a couple of your articles as long as I provide credit and sources back to your webpage? My blog is in the very same area of interest as yours and my visitors would certainly benefit from a lot of the information you present here. Please let me know if this okay with you. Thanks a lot!
Hello there, You’ve performed a great job. I’ll definitely digg it and personally recommend to my friends. I’m confident they’ll be benefited from this website.
Thank you for the auspicious writeup. It actually used to be a entertainment account it. Look advanced to more brought agreeable from you! By the way, how could we keep up a correspondence?
I am not sure where you are getting your information, but good topic. I needs to spend some time learning much more or understanding more. Thanks for fantastic information I was looking for this info for my mission.
It’s really a nice and helpful piece of information. I am glad that you shared this helpful info with us. Please keep us up to date like this. Thanks for sharing.
ivermectin for guinea pigs petsmart worming rabbits with ivermectin
I read this paragraph completely regarding the comparison of latest and preceding technologies, it’s amazing article.
ตัวอย่างซีรีส์จีน หยุนซี มเหสียอดอัจฉริยะแห่งพิษ Musical ภาพยนตร์เพลง เช่น ชิคาโก ประเทศไทยยังไม่มีให้เห็นเป็นเรื่องเป็นราวสักเรื่อง แต่ก็ยากที่จะทำให้มีรายได้เพราะความนิยมของคนแนวนี้ไม่มาก
Enjoyed every bit of your blog article.Really looking forward to read more. Much obliged.
lasix online order – buy betamethasone 20gm sale3 brand betnovate 20gm
Usually I don’t read post on blogs, but I wish to say that this write-up very pressured me to try and do so! Your writing style has been surprised me. Thank you, quite nice article.
gapeworm treatment ivermectin ivermectin for cats fleas
gabapentin 100mg over the counter – clomipramine 50mg usa order itraconazole 100mg without prescription
Fantasy leagues involve bettors’ deciding on actual athletes for a «fantasy team» priorto a contest starts.
เว็บไหนที่ว่าดี เว็บไซต์ไหนที่ว่าเด็ด ผมลองหมดแล้วนะครับ ในตอนนี้มาตกลงใจตรงนี้เลยครับ UFABET จะต้องยอมรับว่าระบบเค้าเยี่ยมสุดแล้วที่ผมเล่นมาก ไม่กระตุกไม่ค้าง ฝากเงินอัตโนมัติ ยิ่งสะดวกรวดเร็วทันใจ ที่สำคัญมีทีมงานรอแนะนำ 24 ชั่วโมง
whoah this blog is excellent i love reading your articles. Stay up the great paintings! You recognize, a lot of persons are looking round for this info, you can aid them greatly.
Paragraph writing is also a excitement, if you be familiar with afterward you can writeotherwise it is complicated to write.
I’d must talk with you here. Which is not something It’s my job to do! I love reading a post that can get people to think. Also, many thanks for permitting me to comment!
great issues altogether, you just won a logo new reader.What would you recommend about your submit that you made a few days in the past?Any certain?
generic prednisolone 40mg – purchase prometrium generic prometrium price
Remarkable! Its truly amazing article, I have got muchclear idea concerning from this paragraph.
azithromycin 250mg usa – tindamax sale buy nebivolol for sale
«I am impressed with this website , rattling I am a big fan .»
Heya i’m for the first time here. I found this board and I find It truly useful & it helped me out a lot.I hope to give something back and help others likeyou helped me.
This is a really good tip especially to thosenew to the blogosphere. Brief but very precise info… Many thanks for sharing this one.A must read article!
Is anyone in a position to recommend comprehensive Hydraulic Valves Business Contact List? Thank you 😀
I cannot thank you enough for the blog post.Really thank you! Cool.
Say, you got a nice article post. Want more.
Really appreciate you sharing this article. Fantastic.
Say, you got a nice article.Really thank you! Great.
Im grateful for the article.Really looking forward to read more. Will read on…
dosage for lasix lasix for horses for sale lasix causes when given abruptly
stromectol usa – stromectol tablet stromectol
How are california bar essays graded studybayUYhjhgTDkJHVy
I need to to thank you for this very good read!! I definitely loved every little bit of it.I have you book-marked to check out new stuffyou post…
Really informative article.Thanks Again. Keep writing.
order amoxil for sale – buy valsartan sale ipratropium 100mcg drug
accutane 40mg us – decadron 0,5 mg cheap buy cheap linezolid
ivermectin 3 mg tablets – carbamazepine 200mg tablet carbamazepine 400mg canada
Some times its a pain in the ass to read what people wrote but this internet site is rattling user pleasant! .
I reckon something truly interesting about your blog so I saved to favorites.
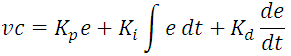
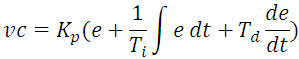
muy buen aporte Gracias!!!
Buen articulo
Saludos!
Hola.
muchas gracias por la aportación.
¿que valores usas para el escalamiento en la instrucción PID?
Saludos!
Buena pregunta. Se dejaron los valores por defecto. Variable de proceso max(4095 – 4095), Min(0 – 0). y para la salida Max(100 – 100), minimo (0-0)
anda ya
Muchas gracias profesor, me ah sido de mucha ayuda su articulo.
Que opinan de herramientas para ajuste de ganancias como:
https://pidtuner.com/
La información esta muy buena. en el párrafo de Ganancias dependientes. la narración confunde cuando dice: » A esta forma de la ecuación se le denomina ecuación de variables dependiente, a diferencia de la ecuación anterior que es conocida como ecuación de variables dependientes.»
Ramón, tiene mucha razón, ya lo corregí. Este tipo de comentarios son lo que hacen posible que los articulos mejoren.
Gracias
en el simens abra un video
Que modelo de Siemens usas?
Excelente información, saludos profe.
Gracias Efrain. Saludos
Gran post.